Curve Number extension
Note
The Curve Number model can be used as an extension to WaTEM/SEDEM. When the CN-module is activated, the model is called CN-WS. CN-WS was developed in 2016 by KU Leuven (in a consortium with Antea group Belgium, see Antea, 2016). This model extension was made to simulate the sediment transport to watercourses and to evaluate the effects of erosion control measures, both in space and time, based on time series of rainfall events. Both models, WaTEM/SEDEM, and the Curve Number model have been used a lot, however there is no published literature on their coupling. See the section on the history for more information about the development history.
Introduction to the Curve number method
The curve number (CN) method is an empirical run-off modelling approach which knows widespread use in the hydrologic community. The low model complexity and limited input requirements explain the popularity of this model, especially in data-scarce areas. The original CN method has been developed in the mid-50’s by the former American Soil Conservation Service (SCS) and has been revised several times since then (NRCS, 2010). Based on field experiments with standardised rectangular run-off plots, local coefficients, so-called ‘curve numbers’ were originally determined and tabulated.These take into account local conditions (soil type and land cover, …) in order to accurately estimate run-off from recorded rainfall input. Important to note is that the output of the original model formulation is event-based, and is thus not temporally nor spatially distributed. However, in larger modeling frameworks in which run-off is only one of the simulated phenomena, a spatio-temporal representation of the model output is common. Therefore, in order to incorporate the curve number approach, a translation of this event-based output is necessary.
In the documentation below the following 2 parts are discussed:
A description of the original CN method
The translation of the original model to the CN-based module which is in use in the CN-WS modelling framework
The original CN method
The main governing assumption of the CN method is the following:
with:
\(Q\): run-off depth (\(m\))
\(P\): rainfall depth (\(m\))
\(I_a\): initial abstractions (e.g. infiltration depth before run-off starts, evaporation, interception)(\(m\))
\(F\): actual loss (effective water storage) (\(m\))
\(S\): potential loss (maximum water storage after run-off starts) (\(m\))
Important to note is that the variables described above, do not represent time series variables. The CN method is an event-based model. All the variables are cumulative depths over an event. The term ‘depth’ indicates water volume per square meter, hence the unit \(m\).
The mass balance implies following equation:
Furthermore \(I_a\) is expressed as a fraction of the potential loss \(S\):
A higher value for the dimensionless constant \(c\) essentially implies that more water is initially ‘lost’ by mainly infiltration and evapotranspiration before the run-off phenomena starts. It was originally set to 0.2, however, the quality of choice has been often questioned. Nowadays it is often put at lower values (Ponce V.M. & Hawkins, 1996), especially in an urbanized context. Combining equations 1, 2 and 3 results in the following expression for \(Q\):
\(S\), finally, can be expressed as a function of the dimensionless curve number \(CN\), an empirical parameter ranging between 0 (everything infiltrates, e.g. a dry very porous soil) and 100 (nothing infiltrates, e.g. a parking lot):
The \(CN\) values can be extracted from tables (NRCS, 2010), based on soil type, land use, hydrologic condition, and initial moisture conditions. Combining last two equations, \(Q\) can thus be expressed solely as a function of \(P\) and \(CN\) like depicted in the graph below (source: USDA technical release 55, urban hydrology for small watersheds)
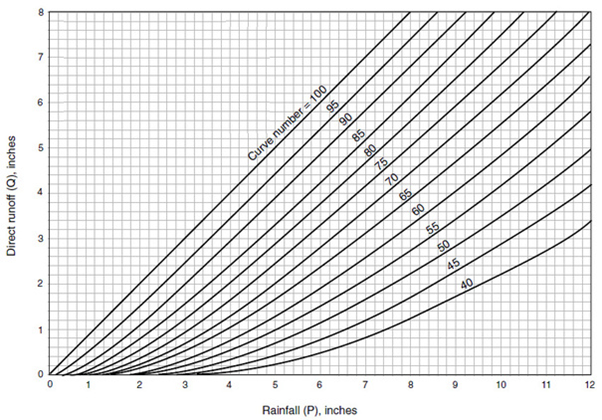
Run-off as a function of rainfall for different CN-values (USDA technical release 55, urban hydrology for small watersheds)
The simplistic nature of the original CN method explains its widespread use. It is important to note that original CN method is best suited for applications in an agricultural context. Furthermore, one has to keep in mind that this method spatio-temporarily lumpes output at the event-scale. Finally, it is important to note that abstraction is made of certain processes like e.g. rainfall intensity, surface crust formation, crop cover, antecedent conditions, etc.
The run-off module used in CN-WS does not represent the original CN method. To overcome these shortcomings mentioned above, some adjustments to the original CN method have been made. On the one hand some processes are incorporated into the equations, on the other hand a spatio-temporal translation of the event-based output is implemented. In the following section the current implementation of the CN-based run-off module is presented.
CN-based extension in WaTEM/SEDEM
For every grid cell the total event-based run-off is calculated based on the local \(CN\) value and the total rainfall depth \(P\) following the original CN-formulation. A first adaptation suggested by Van Oost 2003 is pre-processing the tabulated \(CN\) values so that effects of crop cover and soil crusting are also accounted for:
with:
\(CN_{max}\): the maximum CN derived from the USDA SCS handbook (\(-\))
\(CC\): the percentage of crop cover (\(\%\))
\(c_1\): coefficient related to the crop cover (\(-\))
\(Cr\): the crusting stage (\(-\))
\(c_2\): coefficient related to the crusting stage (\(-\))
The \(c_2\) coefficient is a constant (3), the \(c_2\) coefficient is set in such a way that the calculated CN value is equal to the minimum value derived from the USDA SCS handbook in case of a crop cover of 100%. Soils prone to crust formation tend to be less permeable which results in more run-off generation. The crusting stage \(Cr\) brings this effect into account. More details about this coefficient can be found in Govers et al. (1986).
Furthermore, Van Oost 2003 also suggested a correction factor for the total simulated run-off value using rainfall intensity and antecedent rainfall depth:
with:
\(Q_{CNII}\): the estimated direct run-off using antecedent moisture condition II (\(m\))
\(IN_{max10}\): the maximum 10-minute rainfall intensity (\(m\))
\(AR5\): the 5 days antecedent rainfall depth (\(m\))
\(\alpha, \beta\): tuning parameters (\(-\))
\(CNII\) indicates the standard tabulated curve number value. This value represents the curve number under average soil moisture conditions. A conversion table exists to translate \(CNII\) into \(CNI\) (dry soil) and \(CNIII\) (wet soil). However Van Oost, 2003 opted for the 5 days antecedent rainfall depth \(AR5\) to take into account antecedent wetness conditions.
In grid cells at which the rainfall depth P is lower than the initial abstraction \(I_a\), infiltration is simulated following the equation below (Van Oost, 2003):
with:
\(I\): infiltration (\(m\))
\(D\): duration of the rainfall event. (\(min\))
The total generated run-off is distributed over all timesteps proportional to the rainfall distribution during the event. This results in a generated run-off value for every grid cell at every time step.
Subsequently run-off redistribution through the landscape is modelled stepwise through time. In general, the following 2 steps are considered:
Calculating present run-off in a grid cell at certain timestep t:
with:
\(RO_{tot,t}\): total present run-off volume at timestep \(t\) (\(m^3\))
\(RO_{r,t-1}\): run-off volume still present since previous timestep \(t-1\) (\(m^3\))
\(RO_{P,t}\): run-off volume generated by rainfall during timestep \(t\) (\(m^3\))
\(RO_{in,t-1}\): upstream run-off volume generated at timestep \(t-1\) (\(m^3\))
2) Calculating run-off leaving the grid cell to 1 or 2 neighbouring downstream grid cells based on the routing table:
with:
\(RO_{out,t}\): run-off volume leaving the grid cell towards the neighbouring downstream grid cell at timestep t (\(m^3\))
\(RO_{tot,t}\): total present run-off volume at timestep t (\(m^3\))
\(\alpha\): routing fraction towards the downstream grid cell (\(-\))
\(v\): flow velocity (\(m s^{-1}\))
\(\Delta t\): time step duration (\(s\))
\(d\): flow distance to the downstream grid cell (\(m\))
During the stepwise calculation of the run-off in the catchment the following variables are constantly updated for output at the end of the procedure:
The amount of run-off that leaves the catchment during every time step
Total amount of run-off leaving the catchment
Total amount of run-off passing through each outlet
The amount of run-off that enters every river segment during every time step
The total amount of run-off that enters every river segment
A map with the total amount of run-off for every grid cell for the entire event
The total amount of spillover for each buffer
The total amount of water leaving the system through the sewers
Run-off in special cases
For buffer grid cells, the run-off outflow is calculated in a alternative way. More information about the calculations in buffer can be found here. If in the considered grid cell, a sewer inlet is modelled, a fraction of the run-off will be transported through the sewers. More information about the sewer functionality in the model can be found here.
CN-WS
As stated above, the Curve Number model is combined with WaTEM/SEDEM to simulate sediment transport to a river during a rainfall event. The combination of both models is called CN-WS.
The CN model is used to simulate the run-off as a function of time and space. For every outlet or (optionally) river segment a hydrogram (stream velocity as a function of time) is generated.
WaTEM/SEDEM is used to model the total sediment load leaving the model domain via rivers or an outlet. The use of WaTEM/SEDEM in CN requires to precompute an R-factor and provide it as model input.
The output of both models is combined: the total sediment load is distributed over the hydrogram to obtain a sedigram (sediment concentration and sediment load as a function of time). The sediment concentration \(SC\) is calculated for every timestep as:
With:
\(SC\), the sediment concentration for an event (\(g.l^{-1}\)).
\(SV_{event}\), the total sedimentload for one event (\(kg\)).
\(RO_{event}\), the total run-off volume for one event (\(m^{3}\)).
Do note that the sedigram is constant over an event, but not over a timeseries. The sediment load and flow are integrated over time for a single event, leading to two constants per event. A timeseries is generated by considering different events (see also R-factor python packge).
Additional model features
Some additional functionalities were added to CN-WS, next to the basic model features of WaTEM/SEDEM and the CN model. These additional functionalities have a large impact on water and sediment transport through the model domain. By default, these additional features are disabled, but can be enabled in the ini-file with the correct user choice. When the user enables an extra feature, the model will expect more user input (rasters and variables).
Buffer basins
Buffer basins have a large impact on the dynamics of water and sediment run-off in the landscape. These constructions are temporary storages of water and sediment traps. The delayed water run-off and sediment deposition is included in the model.
In the WaTEM/SEDEM part of CN-WS, all sediment entering the pixels of a buffer is multiplied with the sediment trapping efficiency of the buffer. This trapping efficiency is the fraction of the incoming sediment that is trapped in the buffer basin.
The delayed water run-off is based on the report of Meert and Willems (2013) and uses following principles in the CN-model in CN-WS:
Water will only flow out of a buffer basin when the water height in the basin exceeds the height of discharge pipe of the buffer. Therefore, the dead volume, \(V_{dead}\), is calculated by
Where:
\(H_{opening}\) is the height of the opening of the discharge pipe of the buffer basin \((m)\)
\(H_{dam}\) is the height of the dam of the buffer basin \((m)\)
\(V_{basin}\) is the maximum volume of water that can be trapped in the buffer basin (\(m^{3}\)).
Two cases exist. A first case can be defined as when the water volume in the buffer basin is larger than \(V_{dead}\), but smaller than \(V_{basin}\), the water will flow through the discharge pipe according to
where:
\(R(t)\): the amount of run-off during timestep t (\(m^{3}\))
\(Q_{max}\): the maximum discharge (\(m^{3} s^{-1}\))
\(V(t)\): the volume of water present in the buffer basin at timestep t (\(m^{3}\))
\(dt\): the timestep \((s)\)
\(Q_{max}\) is calculated for every buffer basin according to
Where :
\(C_d\) is the discharge coefficient \((-)\),
\(A_0\) is the area of the discharge opening (\(m^{2}\))
\(g\) is the gravitational acceleration (9.81 \(m.s^{-2}\))
A second case arises when the water volume in the buffer basin is larger than \(V_{basin}\). In this case the water will flow from the basin through the discharge pipe \(R_{opening}\), as well as, via the overflow of the dam \(R_{overflow}\).
Where:
\(W_{dam}\) is the width of the overflow on the buffer basin dam \((m)\)
\(h\) is the height of the water above the overflow \((m)\) and is calculated for every timestep by:
Where \(A_{basin}\) represents the area of the buffer basin in \(m^{2}\)
The practical use of buffer basins in the model is described in a separate section.
Dams and ditches
Dams and ditches influence the direction of water and sediment transport and, thus, alter the routing. The routing along a dam or ditch is incorporated in the routing algorithm. A detailed explanation about these functionalities is given in the user choices sections about ditches and dams.
Sewers/endpoints
Sewers, or more generally, endpoints, are sinks of sediment in the model domain. When sediment is routed to an endpoint, only a fraction of it is transported further downstream. A detailed explanation about this functionality is given in the user choices section about sewers. This feature can be used to incorporate known sediment sinks in the model.
References
Antea, 2016. Modellering van de sedimentaanvoer naar de waterlopen, het effect van erosiebestrijdingsmaatregelen en het transport van sediment in de onbevaarbare waterlopen. Departement Omgeving. Afdeling Gebiedsontwikkeling, Omgevingsplannen en -projecten. Land en Bodembescherming, Brussel. https://www.vlaanderen.be/publicaties/modellering-van-de-sedimentaanvoer-naar-de-waterlopen-het-effect-van-erosiebestrijdingsmaatregelen-en-het-transport-van-sediment-in-de-onbevaarbare-waterlopen
Govers G., 1986, Mechanismen van akkererosie op lemige bodems, unpublished PhD thesis, Faculteit Wetenschappen, KU Leuven.
NRCS, 2010, Chapter 9 Hydrologic Soil-Cover Complexes, National Engineering Handbook Part 630 Hydrology, 20 pp. https://directives.sc.egov.usda.gov/OpenNonWebContent.aspx?content=17758.wba
Ponce V.M. and Hawkins R.H., 1996, Run-off Curve Number: has it reached maturity?, Journal of Hydrologic Engineering, 1: 11-19. https://doi.org/10.1061/(ASCE)1084-0699(1996)1:1(11)
Van Oost, K., Govers, G. & Desmet, P.J.J., 2000, Evaluating the effects of changes in the landscape structure on soil erosion by water and tillage. Landscape Ecology 15, 577-589. https://doi.org/10.1023/A:1008198215674
Van Oost K., 2003, Spatial modeling of soil redistribution processes in agricultural landscapes, unpublished PhD thesis, Faculty of Sciences, KU Leuven.
Van Rompaey, A., Verstraeten, G., Van Oost, K. Govers, G. & Poesen, J., 2001, Modelling mean annual sediment yield using a distributed approach. Earth Surface Processes and Landforms 26(11), 1221-1236. https://doi.org/10.1002/esp.275
Verstraeten, G., Van Oost, K., Van Rompaey, A., Poesen, J. & Govers, G., 2003, Evaluating an integrated approach to catchment management to reduce soil loss and sediment pollution through modelling. Soil Use and Management, 18, 386-394. https://doi.org/10.1111/j.1475-2743.2002.tb00257.x
Verstraeten, G., Poesen, J., Demarée, G., Salles, C, 2006, Long-term (105 years) variability in rain erosivity as derived from 10-min rainfall depth data for Ukkel (Brussels, Belgium): Implications for assessing soil erosion rates. Journal of geophysical research, 111. https://doi.org/10.1029/2006JD007169